The usual way to find the resonant tank capacitor value is to incorrectly assume that the output impedance of the transformer equals the NST rated output voltage divided by the rated output current. This isn't necessarily very accurate because the values printed on the transformer might be for neon tube load.
I present a better (?) way of finding the resonant tank capacitor size using the linear transformer model parameters. This paper relies on A method to determine the Linear Transformer Model parameters of a Neon Sign Transformer paper.
Please note that the formulas were derived by me from scratch, which was a lot of work. If you decide to include the results of my work on your website, please give me due credit and link to http://www.tr-labs.com/
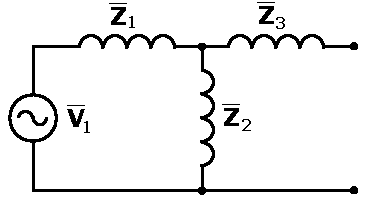
We use the T-equivalent circuit of the linear transformer model. We neglect the wire resistances, because it was shown in A method to determine the Linear Transformer Model parameters of a Neon Sign Transformer that their effect is negligible. If we included them, they would make the calculations A LOT more difficult for nothing. Then we use a series of Thevenin and Norton source transformations in order to find the Thevenin equivalent impedance of the transformer.

where:
V1 = input voltage
Z1
= j(XP-XM)
Z2 =
jXM
Z3 =
j(XS-XM)
First we replace the series combination of the voltage source V1 and the impedance Z1 with the parallel combination of a current source and the Z1 impedance:

where:
![]()
Next, we replace the parallel combination of the current source and impedances Z1 and Z2 with the series combination of a voltage source and impedances:
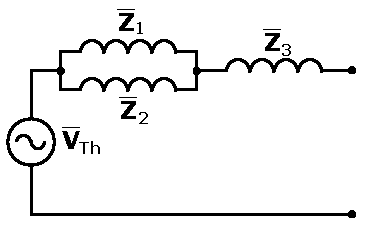
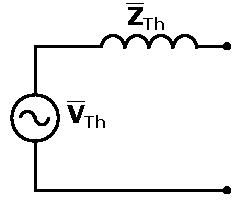
Then we combine the two parallel and one series impedance into a single impedance:
where:
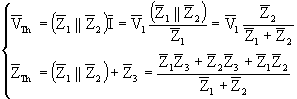
We have managed to reduce the transformer into an ideal voltage source and a single impedance. VTh is the Thevenin equivalent voltage and ZTh the Thevenin equivalent impedance.
Next, we substitute the reactances and simplify:
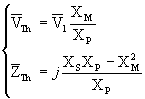
Taking absolute values of both sides and rearranging we yield:
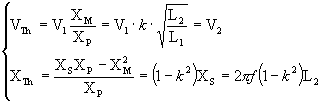
Maximum power transfer theorem states that the maximum power transfer between the voltage source and load occurs when the load impedance equals the complex conjugate of the Thevenin equivalent impedance of the source. In practice this means that the capacitive reactance of the tank capacitor should equal the inductive reactance of the Thevenin equivalent impedance of the transformer:
![]()
We would have arrived exactly at the same formula if we had chosen the capacitor so that it forms a resonant circuit with the Thevenin equivalent impedance at f Hz. This proves our reasoning correct.
Tero’s formula for determining the resonant tank capacitor size using the linear transformer model parameters:
![]()
where:
f = line frequency [Hz]
k = coupling
coefficient
L2 = secondary inductance [H]
The linear transformer model parameters of my 8kV 50mA NST were calculated in A method to determine the Linear Transformer Model parameters of a Neon Sign Transformer
f = 50Hz
k = 0.9053
L2 =
3475H
![]()
We get a somewhat different value going the usual way:
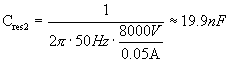
There is a lot research to do in this field. It's still unknown how to analytically determine the most optimal tank capacitor for an NST operated Tesla Coil. By computer simulating the charging circuit, it was found (by Terry Fritz I believe) that about 1.5 times larger capacitor than the resonance value yields the best output. Probably there will never be an analytical way to determine the optimal value, because the voltage and current waveforms become non-sinusoidal when the spark gap is introduced rendering the sinusoidal steady-state analysis useless. The linear transformer model parameters of the NST are ofcourse valid (and very important when doing the computer simulation of the circuit), but the optimal capacitor size has to be determined by brute-force simulation. I'm working on it.