TSSP: Secondary Stress Factors

Last updated: Sat May 11 03:28:23 MDT 2002

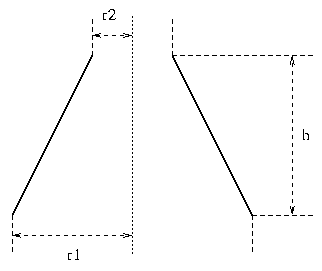
Given a secondary resonator with length h carrying a top voltage Vtop, we can say that the average volts per unit length is Vtop/h.

However, for most secondaries the voltage rise is not uniform and therefore for part of the coil at least, the voltage gradient must exceed this average value. We can compare the actual highest voltage gradient on the coil with the uniform Vtop/h value by defining a voltage stress factor,

Stress factor = Highest gradient / average gradient
This factor is relevant when calculating the maximum volts per turn or volts per unit length for a coil. Given the energy storage capacitance Cee for a coil, the expected peak top voltage for a primary energy E is
Vtop = sqrt( 2 * E / Cee)
When this voltage is divided by length or turns to get the desired peak gradient, the result should be multiplied by the stress factor to take account of the non-uniform voltage rise. The voltage stress factor varies with the shape of the coil, and the purpose of this numerical experiment is to map the variation of this factor.

Calculations are ongoing. This page is automatically updated roughly every hour.

Definitions

This definition of shape factors covers all types of flat, cylinder, and code coils.

Stress factor = highest gradient / average gradient

h = overall height
d = average diameter = r1 + r2
A = h/d
B = (r1 - r2)/d

r1 is the radius across the earthed end of the coil,
r2 is the radius across the hot end.

Results so far

The numbers show the highest and lowest stress factor for coils of that shape. n = number of coils tested.

Results for coils at elevation 2 * d
B
A -1.0-0.8-0.5-0.3 0.0 0.3 0.5 0.8 1.0
0: 1.83
1.76
n=6		1.68
1.57
n=6		1.41
1.33
n=4		1.29
1.18
n=3

1.32
1.31
n=3		1.55
1.53
n=4		1.93
1.91
n=6		2.19
2.14
n=6
1.0: 1.95
1.83
n=6		1.81
1.65
n=7		1.47
1.39
n=6		1.33
1.26
n=6		1.27
1.23
n=6		1.51
1.47
n=6		1.74
1.69
n=6		2.07
2.03
n=7		2.27
1.24
n=7
1.5: 1.98
1.87
n=6		1.76
1.70
n=6		1.56
1.42
n=6		1.40
1.28
n=6		1.30
1.26
n=6		1.61
1.54
n=6		1.81
1.78
n=6		2.16
2.12
n=6		2.37
2.31
n=6
2: 1.96
1.91
n=6		1.78
1.74
n=6		1.56
1.45
n=6		1.45
1.30
n=6		1.32
1.28
n=6		1.63
1.61
n=6		1.90
1.85
n=6		2.24
2.20
n=6		2.42
2.39
n=6
2.5: 2.07
1.95
n=7		1.92
1.77
n=7		1.61
1.48
n=7		1.46
1.30
n=7		1.40
1.31
n=7		1.70
1.66
n=7		1.93
1.92
n=7		2.28
2.26
n=7		2.48
2.46
n=7
3: 2.09
1.97
n=7		1.89
1.79
n=7		1.58
1.48
n=7		1.40
1.29
n=7		1.41
1.33
n=7		1.74
1.70
n=7		2.02
1.97
n=7		2.38
2.31
n=7		2.56
2.50
n=7
4: 2.09
2.02
n=7		1.95
1.82
n=7		1.59
1.49
n=7		1.35
1.29
n=7		1.40
1.34
n=7		1.82
1.76
n=7		2.06
2.04
n=7		2.44
2.40
n=7		2.63
2.60
n=7
6: 2.20
2.06
n=6		1.99
1.85
n=6		1.58
1.51
n=6		1.36
1.30
n=6		1.40
1.37
n=6		1.86
1.85
n=6		2.18
2.15
n=6		2.55
2.53
n=6		2.75
2.73
n=6
8: 2.22
2.06
n=5		1.95
1.88
n=5		1.61
1.49
n=5		1.43
1.28
n=5		1.43
1.39
n=5		1.92
1.91
n=5		2.24
2.22
n=5		2.63
2.62
n=5		2.84
2.80
n=5
10: 2.16
2.08
n=5		2.00
1.87
n=5		1.52
1.51
n=5		1.34
1.29
n=5		1.43
1.41
n=5		1.96
1.95
n=5		2.31
2.28
n=5		2.69
2.68
n=5		2.89
2.88
n=5

Results for coils at elevation 0.5 * d
B
A -1.0-0.8-0.5-0.3 0.0 0.3 0.5 0.8 1.0
0: 1.81
1.71
n=6		1.58
1.53
n=6		1.33
1.29
n=4		1.22
1.17
n=3

1.36
1.32
n=3		1.58
1.54
n=4		1.94
1.92
n=6		2.19
2.16
n=6
1.0: 1.93
1.23
n=7		1.77
1.64
n=7		1.53
1.40
n=6		1.38
1.26
n=6		1.26
1.23
n=6		1.54
1.48
n=6		1.72
1.70
n=6		2.08
2.05
n=7		2.29
1.23
n=7
1.5: 1.96
1.85
n=6		1.73
1.68
n=6		1.53
1.42
n=6		1.38
1.27
n=6		1.34
1.27
n=6		1.63
1.56
n=6		1.85
1.79
n=6		2.19
2.14
n=6		2.39
2.34
n=6
2: 2.05
1.90
n=6		1.80
1.72
n=6		1.51
1.44
n=6		1.39
1.30
n=6		1.31
1.29
n=6		1.68
1.62
n=6		1.89
1.87
n=6		2.25
2.21
n=6		2.45
2.41
n=6
2.5: 2.04
1.93
n=7		1.88
1.75
n=7		1.57
1.47
n=7		1.41
1.29
n=7		1.33
1.30
n=7		1.71
1.67
n=7		1.96
1.93
n=7		2.31
2.28
n=7		2.52
2.47
n=7
3: 2.08
1.96
n=7		1.85
1.78
n=7		1.54
1.47
n=7		1.36
1.29
n=7		1.36
1.32
n=7		1.73
1.71
n=7		2.02
1.98
n=7		2.36
2.33
n=7		2.55
2.53
n=7
4: 2.07
2.00
n=7		1.92
1.81
n=7		1.55
1.49
n=7		1.40
1.29
n=7		1.39
1.35
n=7		1.81
1.78
n=7		2.12
2.06
n=7		2.46
2.42
n=7		2.63
2.62
n=7
6: 2.19
2.05
n=6		1.99
1.84
n=6		1.55
1.48
n=6		1.36
1.30
n=6		1.44
1.39
n=6		1.90
1.87
n=6		2.20
2.17
n=6		2.57
2.55
n=6		2.78
2.75
n=6
8:

1.93
1.86
n=5		1.65
1.48
n=5		1.40
1.29
n=5		1.45
1.41
n=5		1.94
1.92
n=5		2.26
2.24
n=5		2.68
2.63
n=5

10: 2.15
2.07
n=5		1.99
1.86
n=5		1.50
1.49
n=5		1.34
1.29
n=5		1.47
1.42
n=5		2.00
1.96
n=5		2.31
2.29
n=5		2.71
2.70
n=5		2.92
2.90
n=5

Inductance factor

The ratio Les/Ldc. We get these as a free byproduct of the calculation, so we might as well plot them.

Results for coils at elevation 2 * d
B
A -1.0-0.8-0.5-0.3 0.0 0.3 0.5 0.8 1.0
0: 1.19
1.19		1.20
1.20		1.28
1.27		1.40
1.40
1.63
1.63		1.49
1.48		1.39
1.38		1.36
1.35
1.0: 1.17
1.16		1.15
1.15		1.14
1.14		1.14
1.14		1.15
1.15		1.17
1.17		1.19
1.18		1.23
1.22		1.25
1.15
1.5: 1.14
1.13		1.11
1.11		1.08
1.07		1.06
1.05		1.05
1.04		1.06
1.06		1.09
1.08		1.14
1.14		1.18
1.17
2: 1.11
1.10		1.08
1.08		1.03
1.02		1.00
1.00		0.98
0.97		1.00
0.99		1.03
1.02		1.08
1.07		1.12
1.11
2.5: 1.08
1.08		1.05
1.04		0.99
0.98		0.96
0.95		0.93
0.93		0.95
0.94		0.98
0.97		1.04
1.03		1.08
1.07
3: 1.05
1.05		1.02
1.01		0.96
0.95		0.92
0.92		0.90
0.89		0.92
0.91		0.95
0.94		1.01
1.00		1.04
1.03
4: 1.01
1.01		0.97
0.97		0.91
0.90		0.87
0.87		0.86
0.85		0.88
0.87		0.91
0.90		0.96
0.95		0.99
0.98
6: 0.95
0.95		0.91
0.90		0.85
0.84		0.82
0.81		0.81
0.80		0.83
0.82		0.86
0.85		0.91
0.90		0.94
0.93
8: 0.91
0.90		0.87
0.86		0.81
0.80		0.78
0.77		0.78
0.77		0.81
0.80		0.84
0.83		0.89
0.87		0.91
0.89
10: 0.88
0.87		0.84
0.83		0.79
0.77		0.76
0.75		0.77
0.75		0.80
0.78		0.83
0.81		0.88
0.86		0.89
0.88

Results for coils at elevation 0.5 * d
B
A -1.0-0.8-0.5-0.3 0.0 0.3 0.5 0.8 1.0
0: 0.99
0.99		1.01
1.01		1.09
1.08		1.19
1.19
1.29
1.29		1.14
1.13		1.02
1.01		0.99
0.98
1.0: 1.07
1.03		1.06
1.06		1.05
1.05		1.04
1.04		1.04
1.03		1.03
1.02		1.02
1.01		1.01
1.00		1.03
1.00
1.5: 1.06
1.06		1.04
1.04		1.00
1.00		0.98
0.97		0.95
0.95		0.95
0.94		0.95
0.95		0.97
0.96		0.98
0.97
2: 1.05
1.05		1.02
1.01		0.96
0.96		0.93
0.93		0.90
0.90		0.90
0.89		0.91
0.91		0.94
0.93		0.95
0.94
2.5: 1.03
1.03		0.99
0.99		0.93
0.93		0.90
0.89		0.87
0.86		0.87
0.86		0.88
0.88		0.91
0.91		0.93
0.92
3: 1.01
1.01		0.97
0.97		0.91
0.90		0.87
0.87		0.84
0.84		0.85
0.84		0.86
0.86		0.90
0.89		0.91
0.90
4: 0.98
0.97		0.94
0.93		0.87
0.86		0.83
0.83		0.81
0.80		0.82
0.81		0.84
0.83		0.87
0.86		0.89
0.88
6: 0.93
0.92		0.88
0.88		0.82
0.81		0.79
0.78		0.77
0.76		0.79
0.78		0.81
0.80		0.85
0.84		0.86
0.85
8:
0.85
0.84		0.79
0.78		0.76
0.75		0.75
0.74		0.78
0.76		0.80
0.79		0.84
0.82
10: 0.86
0.85		0.83
0.81		0.77
0.75		0.74
0.73		0.74
0.72		0.77
0.75		0.80
0.78		0.83
0.82		0.85
0.83

Total coils: 1063